5. ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ВЫСОКОСКОРОСТНОГО ВЗАИМОДЕЙСТВИЯ ТЕЛ С БОЛЬШИМИ ДЕФОРМАЦИЯМИ СРЕДЫ В ЭЙЛЕРОВЫХ ПРОСТРАНСТВЕННЫХ ПЕРЕМЕННЫХ
Предлагаемая ниже методика расчета предназначается для компьютерного моделирования процессов высокоскоростного взаимодействия деформируемых тел и их разрушения. При описании напряженно-деформированного состояния взаимодействующих тел используется упругопластическая модель сплошной среды с учетом изменения ее пористости [1, 2]. Численное решение конкретных прикладных задач осуществляется с помощью эйлерового численного метода [3], основанного на конечно-разностной схеме Мак-Кормака и методе маркеров. Этот мтод позволяет исследовать большие деформации взаимодействующих тел, имеющих различные физико-механические свойства. Первый вариант этого метода был применен для моделирования ударного взаимодействия тел, имеющих одинаковые физико-механические свойства [4].
Весь комплекс вычислительных алгоритмов и уравнений в дальнейшем будет называться расчетно–математической моделью. В замкнутую систему расчетно-математической модели входят соотношения, которые вычисляются с помощью отдельных алгоритмов. К таким алгоритмам относятся: снос напряженного состояния на поверхность текучести путем корректировки компонент девиаторной части тензора напряжений; вычисление давления и пористости при совместном расчете уравнения состояния и соотношения, задающего закон изменения пористости в зависимости от давления; расчет параметров на фронте детонационной волны и т.д.
Данная работа выполнена при поддержке грантов РФФИ № 05-08-01196а, 06-08-00903а и в рамках целевой программы Федерального агентства по образованию, проект РНП 2.1.2.2398.
5.1. Расчетно-математическая модель упругопластической среды с учетом изменения пористости и разрушения
При математическом моделировании динамических процессов важным этапом является корректное формулирование полной системы уравнений, используемой физической модели. В рамках механики сплошной среды любая модель включает в себя законы сохранения и определяющие соотношения, описывающие свойства конкретных материалов. Математическая модель сплошной среды, используемая при компьютерном моделировании, должна обладать следующими свойствами: адекватно описывать физику процесса; не должна быть чрезмерно громоздкой; допускать эффективную реализацию ее с помощью численных методов; иметь незначительное число легко определяемых параметров.
Излагаемая в данной работе модель упругопластической среды обладает всеми перечисленными выше свойствами. Она при необходимости трансформируется в модель идеальной или вязкой сжимаемой жидкости; в модель пористой упругопластической среды; в модель сыпучих материалов, и т.д. При изложении основной системы уравнений, начальных и граничных условий предполагаются следующие общепринятые для задач высокоскоростного соударения и взрыва ограничения:
- не учитывается влияние силы тяжести и атмосферного давления, т.е. все компоненты тензора напряжений внутри не нагруженных тел равны нулю, а на свободных поверхностях отсутствуют нормальные напряжения;
- взаимодействующие тела, находящиеся в жидкой фазе (вода, расплавленные материалы) моделируются идеальной сжимаемой жидкостью;
- все рассматриваемые материалы являются деформируемыми.
Для отдельных специфических задач эти ограничения могут быть сняты. Однако снятие этих ограничений не приводит к качественно новым результатам. Влияние атмосферного давления и силы тяжести на столько мало, что их учет во многих задачах высокоскоростного удара и взрыва теряет всякий смысл.
Законы сохранения массы, количества движения и энергии. При записи интегральных законов сохранения и других уравнений предполагается, что рассматриваемая сплошная среда однородная, изотропная, процессы рассматриваются адиабатические. В предположении осесимметричности решаемых задач, т.е. независимости всех искомых функций от угла φ цилиндрической системы координат (r, z, φ), основная система уравнений интегральных законов сохранения массы, количества движения и энергии, имеет вид
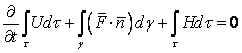 (5.1) (5.1)
Подробное оглавление раздела 5 смотрите здесь, а полное содержание подраздела 5.1 можно скачать здесь.
|